一次元定常熱伝導では、$\partial \theta / \partial t = 0$ とすることで壁を通る熱量$q$ と、複層の場合の熱コンダクタンス$C$ の式を下のように導きました。
$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}$
$q = C \left( \theta _{si} - \theta _{so} \right)$
これを用いて実際に計算を行ってみましょう。
問題は3つ用意しました。使う数値は表にまとめておいたので参考にしてください。ちなみに図中の数字は全てmm(ミリメートル)です(一般的に単位のないものはmmなので)。
○問題 表1、2を利用して各壁体の熱コンダクタンスを求めなさい。
| 材料名称 | 熱伝導率[W/mK] |
|---|---|
| 普通コンクリート | 1.1 |
| 合板 | 0.15 |
| モルタル | 1.3 |
| プラスターボード | 0.14 |
| 材料名称 | 熱抵抗[m^2 K/W] |
|---|---|
| 中空層(厚さ20以上、現場施行) | 0.075 |
 (2)
(2)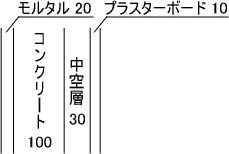 (3)
(3)
--- 以下は解説です。 ---
単位に注意して計算しましょう。まず、熱伝導率の単位はW/mK でワットパーメートルケルビンです。熱抵抗の単位はm^2 K/W 平方メートルケルビンパーワットとなっています。
(1)コンクリートの厚さと熱伝導率から熱コンダクタンスを求めるだけです。
$C = \lambda / l = 1.1 / 0.18 = 6.1 $
(2)複層になっているので、まずは各層の熱コンダクタンスを求めて逆数をとります。
$C_1 = 1.3 / 0.02 = 65,$ $1/C_1 = 0.015$
$C_2 = 1.1 / 0.1 = 11,$ $1/C_2 = 0.091$
$C_3 = 0.14 / 0.01 = 14,$ $1/C_4 = 0.071$
あとは、上で示した式と同じように和をとればいいのですが、中空層があるのでその分の熱抵抗も加えます。
$1/C = 0.015 + 0.091 + 0.075 + 0.071 = 0.252$
結局、熱コンダクタンスは次のようになります。
$C = 3.97$
(3)これは(2)よりも簡単ですね。これまでと同様に解きます。
$C_1 = C_3 = 0.15 / 0.005 = 30$
$1/C_1 = 1/C_3 = 0.033$
$1/C = 0.033 + 0.075 + 0.033 = 0.141$
$C = 7.09 $
以上です。
中空層は熱抵抗で与えられていることが多いので、厚みが増すと厚さに関係なくなることが特徴です。熱コンダクタンスと熱抵抗の関係は逆数になっているだけなので、その点にさえ注意すれば複層の熱コンダクタンスを求めることなんて簡単と感じたのではないでしょうか?
次回は、熱コンダクタンスではなく熱貫流率の話になります。