三次元拡散方程式は拡散方程式のところでふれたように
$\frac{\partial C}{\partial t} = D \left( \frac{\partial ^2 C}{\partial x^2} + \frac{\partial ^2 C}{\partial y^2} + \frac{\partial ^2 C}{\partial z ^2} \right)$
というものでした。また、この式の解は$C\left( x,y,z,t \right) = \frac{M}{\left( \sqrt{ 4 \pi Dt} \right)^3 } \exp \left[ - \frac{x^2 + y^2 + z^2}{4Dt} \right]$
です。今回はこれに流れがあるものを考えてみます。状況は下の図のようなものです。全て書き込むとわけがわからなくなってしまうので省略してあります。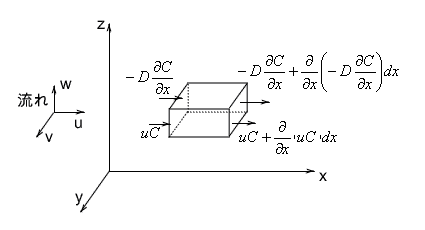
x方向に関してだけ書いてあります。すると、x方向の拡散フラックスは
$D \frac{\partial ^2 C}{\partial x^2} dx dy dz dt$
でした。また、流れによって入ってくる物理量は$\left[ uC - \left( uC+\frac{\partial u C}{\partial x} dx \right) \right] dy dz dt = - \frac{ \partial u C}{\partial x} dx dy dz dt$
となります。y方向、z方向についても同様にすると○y方向
$D \frac{\partial ^2 C}{\partial y^2} dx dy dz dt$
$\left[ vC - \left( vC+\frac{\partial v C}{\partial y} dy \right) \right] dx dz dt = - \frac{ \partial v C}{\partial y} dx dy dz dt$
○z方向$D \frac{\partial ^2 C}{\partial z^2} dx dy dz dt$
$\left[ wC - \left( wC+\frac{\partial w C}{\partial z} dz \right) \right] dx dy dt = - \frac{ \partial w C}{\partial z} dx dy dz dt$
となります。後は一次元のときと同様に箱の中の濃度変化と、上で求めたものの和をとれば終了です。
$\frac{\partial C}{\partial t} dx dy dz dt = D \left( \frac{\partial ^2 C}{\partial x^2} + \frac{\partial ^2 C}{\partial y^2} + \frac{\partial ^2 C}{\partial z^2} \right) dx dy dz dt$
$- \left( \frac{\partial uC}{\partial x} + \frac{\partial vC}{\partial y} + \frac{\partial wC}{\partial z} \right) dx dy dz dt$
これを整理すると
$\frac{\partial C}{\partial t} + \frac{\partial uC}{\partial x} + \frac{\partial vC}{\partial y} + \frac{\partial wC}{\partial z} = D \left( \frac{\partial ^2 C}{\partial x^2} + \frac{\partial ^2 C}{\partial y^2} + \frac{\partial ^2 C}{\partial z^2} \right)$
が得られます。この式は移流拡散方程式と呼ばれています。左辺第一項を時間変化項もしくは非定常項、第二項から第四項までを移流項、右辺を拡散項といいます。この式では移流項があるので線型方程式ではなくなることに注意してください。