波のエネルギーは一波長分の位置エネルギーと運動エネルギーの和の平均値で表されます。つまり、単位面積当たりのエネルギーを波のエネルギーとするということです。順番は位置エネルギーと運動エネルギーを別々に求めていきます。まずは波のエネルギーから考えて見ましょう。下の図を見てください。
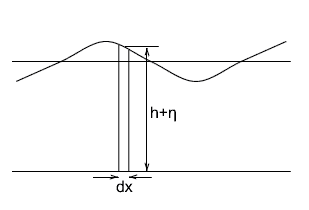
上の図で幅が$dx$の水柱が描かれています。この波の平均水深を$h$、振幅を$\eta$とするとこの水柱の水面までの高さは$h+\eta$と書くことができます。この水柱の持つ位置エネルギーは
$dE_p = \frac{1}{2} \rho g \left( h+\eta \right) ^2 dx$
となります。これを一波長分積分して平均をとれば波の位置エネルギーが求まるので
$E_p = \frac{1}{L}\int ^{x+L}_x dE_p$
を計算すればいいことになります。そこで、これと上で求めた水柱のエネルギーを合わせると
$E_p = \frac{\rho g}{2L} \int^{x+L}_x \left[ h^2 + hH \cos \left( kx-\sigma t \right) + \frac{1}{4}H^2 \cos ^2 \left( kx-\sigma t \right) \right] dx$
となります。これを積分すると
$E_p = \frac{1}{2} \rho gh^2 + \frac{1}{16} \rho g H^2 $
が得られます。しかし、これは波のエネルギーだけでなく波がないときの位置エネルギーも含んでいます。そこで、波がないときのエネルギーは上で$\eta = 0$とすればいいだけなので
$E_p = \frac{1}{2} \rho gh^2$
と簡単に求まります。なので結局波の持つ位置エネルギーは
$E_p = \frac{1}{16} \rho gH^2$
と求まります。
次に運動エネルギーを考えます。まずは下の図を見てください。
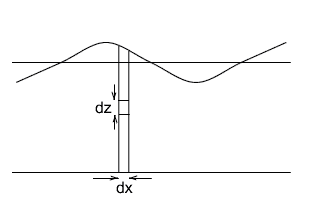
図の中の$dx \cdot dz$の要素について考えます。この部分の運動エネルギーは
$dE_k = \frac{1}{2} \rho \left( u^2 + w^2 \right) dxdz$
となります。ここで、水粒子の運動でやった水粒子の速度を代入すると
$dE_k = \frac{1}{8}\frac{\rho g^2 k^2 H^2}{\sigma ^2 \cosh ^2 \left( kh \right)}$
$\left[ \cosh ^2 \left\{ k \left( h+z \right) \right\} \cos ^2 \left( kx - \sigma t \right) + \sinh ^2 \left[ k \left( h+z \right) \right] \sin ^2 \left( kx-\sigma t \right) \right] dxdz $
となります。ここで双曲線関数、三角関数の公式と
$\sigma ^2 = gk \tanh \left( kh \right) $
を用いて整理すると
$dE_k = \frac{1}{8} \frac{\rho gkH^2}{\sinh \left( 2kh \right)} \left[ \cosh \left\{ 2k \left( h+z \right) \right\} + \cos \left\{ 2 \left( kx-\sigma t \right) \right\} \right]$
となります。この式を$x$は$x \sim x+L$まで、$z$は$-h \sim \eta$まで積分して平均をとればいいのですが、微小振幅波の仮定から$\eta \simeq 0$とすることができるので、この仮定の下での計算は
$E_k = \frac{1}{L} \int ^0_{-h} \int ^{x+L}_x dE_k $
をとけばいいので、代入して解いていくと
$E_k = \frac{1}{8} \frac{\rho gkH^2}{\sinh \left( 2kh \right)} \int ^0_{-h} \cosh \left[ 2k \left( h+z \right) \right] dz$
となります。
次に$z$について積分すると
$E_p = \frac{1}{16} \rho gH^2$
が得られます。結局、運動エネルギーは位置エネルギーと同じ結果になりました。
単位面積当たりの波のエネルギーは
$E = E_p + E_k = \frac{1}{8}\rho gH^2$
となります。求めるまではかなり多くの文字を扱ってきましたが、結局波のエネルギーは波高だけで決まってしまいます。