拡散方程式の解の利用（２）

今回は、場に流れがある場合と反射壁がある場合を考えます。

まず、場に流れがある場合ですが、乱流なんかを想定するのは不可能なので全く乱れのない流れを想定します。全く乱れのない場合は、正弦波の方程式と同じような要領で、拡散方程式の解に流れの要素を踏まえます。

とりあえず、流れを踏まえた拡散方程式の解の形は

次に反射壁を考えます。反射壁を考えるときノイマン型境界条件を考えます。簡単に説明すると、境界において何らかの物理量の勾配が０になるというものです。ここの場合は濃度勾配が０になると考えます。このような考え方の裏づけがある程度にだけ記憶しておいてください。（専門的に学ぶ上で必要になった場合は勉強してください(^^)）

ノイマン型境界条件を考えるとは言いましたが、直感的に考える上では特に意識する必要はありません。拡散に反射壁を考える必要があるときは、仮想放出源を考えてください。（はじめからこれだけ言ってしまったほうがわかりやすかったかな？）仮想放出源は下の図を見ればわかると思います。

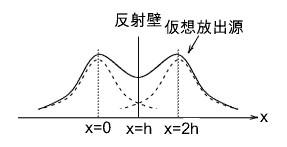
もちろん以前の図の使い回しです。このとき、$x=0$の放出源が実際に放出されているところです。そして、$x=h$に反射壁があり、その反射壁に関して対称に仮想放出源を考えます。すると、自動的に反射壁の位置で濃度勾配が０になります。このようにして、拡散を考えるということは前の拡散方程式の応用（１）と同じ式の形になるということです。

前と異なることは、以前の式は全てのｘについて意味のあるものでした。しかし、今回は$x>h$においては物理的な意味はありません。そのような意味で、以前の式と今回の式は異なっています。

それでは、最後に今回の拡散方程式の解を示して終わります。