全静水圧の大きさと作用位置についてやっていきます。全静水圧とは、ある面に働く合力のことです。下の図を見てください。
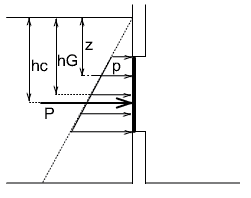
太い縦線が今考えようとしている面です。これに対して、静水圧が斜めの点線のような分布でかかっています。このとき、面に作用している静水圧は斜めの実線です。静水圧は
$p=\rho gz$
で求められました。$h_G$ は考えている面の図心です。図心がわかれば
$P=\rho gh_G A$
から全静水圧の大きさが求められます。これは簡単ですね(^^)
さて、問題はこの全静水圧がどの位置に作用するかということです。その作用位置は
$h_C = h_G + \frac{I_0}{h_G A}$
で求められます。$I_0$ は平板の断面二次モーメントで、 $A$ は平板の面積です。ここが問題です。水理学をならう学年で、断面二次モーメントにはまだ出会っていなんじゃないでしょうか?断面二次モーメントは
$I_0 = \int _A z^2 dA$
で求められます。これでもまだ厳しいかもしれません…(;^^A ということで、もう一段階簡単にすると
$I_0 = \int _z b\left( z \right) z^2 dz$
になります。これでわかりますか? $b\left( z \right)$ となっているのは、幅は常に一定とは限らないからです。三角形の板だったら上から下までたどったときに幅が変わるでしょ?
断面二次モーメントは上に上げたように求めればいいんですが、それでも面倒になってくると思います。そんなときには、暗記で済ませましょう。代表的な形の図形とその断面二次モーメントを表にしたので覚えちゃってください。
| 図形 | 図心 | 図心まわりの断面 二次モーメント |
|---|---|---|
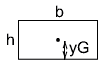 |
$\frac{h}{2}$ |
$\frac{bh^3}{12}$ |
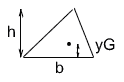 |
$\frac{h}{3}$ |
$\frac{bh^3}{36}$ |
これ以外の図形は、覚えるよりも実際に計算したほうがいいでしょう。あまり暗記に頼ると、いざというときに断面二次モーメントを求められなくなるので注意してください。